Wei-Wei Pan et al. / Physical Review Letters, 2019
Физики из Швеции и Китая впервые напрямую измерили волновую функцию разделенных в пространстве состояний — поляризаций двух запутанных фотонов. Для этого ученые модифицировали метод слабых измерений, заменив слабые значения модулярными. Ранее измерить волновую функцию таких состояний удавалось только с помощью квантовой томографии. Статья опубликована в Physical Review Letters, кратко о ней сообщает Physics.
Как правило, для измерения волной функции системы физики используют квантовую томографию — изготавливают и измеряют много копий системы, а потом восстанавливают коэффициенты разложения волновой функции по базисным состояниям. При этом важно, чтобы измерения проводились в разных базисах — в противном случае информация о фазе волновой функции потеряется, и из полученных результатов получится достать только плотность вероятности (то есть квадрат волновой функции). Оба этих усложнения связаны с принципом неопределенности Гейзенберга, который связывает неопределенности двух дополнительных наблюдаемых (то есть наблюдаемых, операторы которых не коммутируют). Самый простой пример таких наблюдаемых — это координата и импульс. Если мы попытаемся точно измерить положение частицы, то мы непроизвольно «толкнем» частицу и увеличим неопределенность ее импульса. Таким образом, волновая функция частицы после измерения изменится непредсказуемым образом, и достать информацию об исходном состоянии будет невозможно.
Впрочем, квантовая томография — это не единственный способ обойти ограничения квантовой механики и измерить волновую функцию системы. Альтернативой ему служит метод слабых измерений, разработанный в 1988 году Якиром Аароновым, Давидом Альбертом и Львом Вайдманом. Грубо говоря, в этом методе измерительный прибор очень слабо возбуждает систему, извлекая небольшое количество информации о ее состоянии. Результат, полученный в результате такого измерения, называют «слабым значением» некоторой наблюдаемой. Чтобы усилить этот эффект, не разрушая квантовое состояние системы, физики специальным образом «просеивают» начальные и конечные состояния, полученные в многократных реализациях процесса. Важно отметить, что слабые измерения позволяют напрямую получить информацию о волновой функции, минуя этап реконструкции из квантовой томографии.
На практике метод слабых измерений впервые реализовала в 2011 году группа физиков под руководством Джефа Лундина (Jeff Lundeen), определившая с его помощью волновую функцию отдельного фотона. Еще несколько лет спустя та же группа распространила метод на систему из двух квантовых состояний — ортогональные поляризации одного фотона.
Впрочем, у метода слабых измерений есть один существенный недостаток: состояния измеряемой системы не могут быть разделены в пространстве. Это связано с тем, что для стандартной реализации метода все состояния должны возмущаться в один и тот же момент времени. Реализовать такое мгновенное дальнодействие на практике невозможно. В принципе, обойти этот недостаток можно с помощью многократных слабых измерений, однако с помощью такого метода полную информацию о системе получить нельзя. Поэтому для измерения волновой функции таких систем приходится возвращаться к квантовой томографии.
Группа физиков под руководством Гуан-Цань Го (Guang-Can Guo) распространила метод слабых измерений на системы с пространственно разделенными состояниями, заменив слабые значения наблюдаемых модулярными значениями. Чтобы получить такое значение, нужно спроектировать на начальное и «просеянное» состояние не сам оператор, отвечающий наблюдаемой величине, а некоторую функцию от него. Также ученые применили этот метод для двух запутанных фотонов — таким образом, исследователи впервые напрямую измерили волновую функцию двух запутанных состояний, разделенных в пространстве.
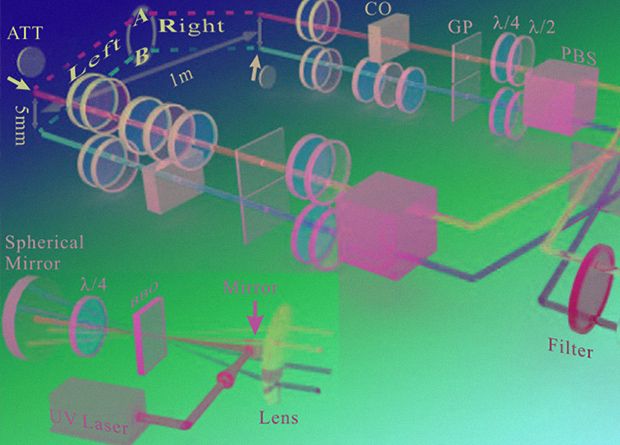
Чтобы сгенерировать запутанные фотоны, ученые светили ультрафиолетовым лазером на кристалл бета-бората бария, который превращал отдельные фотоны в фотонные пары с запутанной поляризацией и импульсом. Затем ученые измерили модулярное значение и восстановили волновую функцию запутанных поляризаций, используя в качестве «счетчика запутанности» (entangled meter) пути, по которым фотоны шли через установку. Грубо говоря, в этом методе вероятность обнаружить «счетчик» в некотором состоянии однозначно связана с действительной и мнимой частью модулярных значений операторов проекции на состояние с заданной поляризацией каждого фотона, а модулярные значения однозначно связаны с волновой функцией запутанных состояний. Для измерения вероятностей ученые использовали интерферометр Франсона, а поляризацией фотонов управляли с помощью поляризационных пластинок. В результате ученые получили волновую функцию запутанных поляризаций, которая хорошо согласуется с томографическими измерениями.

Схема измерения волновой функции запутанных состояний (a) и ее реализация на примере запутанных фотонов
Wei-Wei Pan et al. / Physical Review Letters, 2019

Схема экспериментальной установки
Wei-Wei Pan et al. / Physical Review Letters, 2019
С каждым годом физикам удается измерить свойства волновых функций все более и более сложных систем. Например, в октябре 2017 года исследователи из Австрии и Германии научились регистрировать изменение фазы волновой функции двухчастичной системы, отвечающее перестановке частиц. В январе 2018 другая группа физиков впервые измерила квадрат волной функции электрона в молекуле водорода. Для этого ученые разрушали молекулу с помощью высокоэнергетического пучка света, ловили образовавшиеся продукты распада и восстанавливали по этим данным корреляционные функции. А в июле 2019 шотландские физики впервые «сфотографировали» запутанные фотоны в момент неопределенности их физических состояний.
Дмитрий Трунин
Источник: N+1